2/8.归结一下，你就知道
“唯一性、局部有界性、局部保号性、保不等式性、迫敛性、四则运算……”矽靠在窗边想到，手里拿着纸，“都和数列的极限很相似嘛。”
此时打扫的工作已经结束了，班里的人都在屋内外准备晚餐，因此二楼的房间空了下来，矽得以有这个空档学习数学，而他带来的Pur麦粉已经交给苉去处理了。幸而是在夏日，天暗得晚，在这个东（偏北）的男生的房间里（矽怎么可能会跑到光照更好的女生卧室呢），唯有靠北的窗户还可以照来一点阳光，矽就坐在了这个角落。
“海涅定理……”矽又开始自言自语起来，“设函数f在领域U°(x_0;δ′)内有定义。lim(x→x_0)f(x)存在的充要条件是：对任何含于 U°(x_0;δ′)且以x_0为极限的数列{x_n}，极限 lim(n→+∞)f(x_n)都存在且相等……（归结原则）”
“领域内的都以x_0为极限的数列，其函数值的极限也相等……由于这些数列都趋近于x_0，那 lim(n→+∞)f(x_n)不就相当于f(x_0)嘛，这不是很正常的现象吗？”
“以你的话，可能会感觉这个条件会一直成立。的确，这很普遍，但是也有特例存在，比如：极限 lim(x→0)sin(1/x)不存在。”Isle的纸上这样写道。
“sin(1/x)……”矽挠挠头，继续看纸。
“想必你会在思考sin(1/x)的图像吧。”Isle写道，“sin(1/x)并非周期函数，但是它也是上下波动的，我们来看看它的图像：
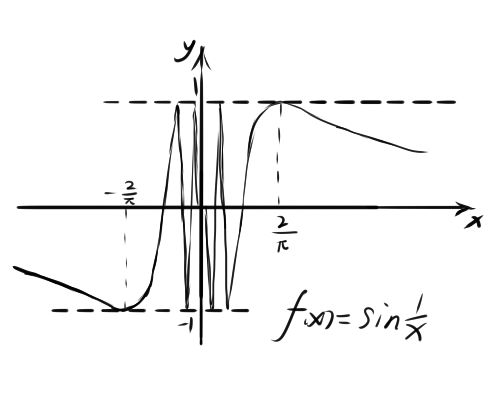。”“由图像我们可以发现（其实考察式子本身也可以发现），在x→0时，sin(1/x)的值不停地上下波动，而且随着x的减小，上下波动的速度越来越快……”
矽想到：“所以说，不能确定在x趋于0时sin(1/x)是趋于区间[-11]间的哪一个值了。”
“……那么现在你应该有所理解了吧。”纸上这样写着，“然后，我们再用代数的方法去证明这个极限不存在，就利用‘归结原则’。”
“要开始了。”矽把纸拿进眼前，越发专注地观察起下面的式子。
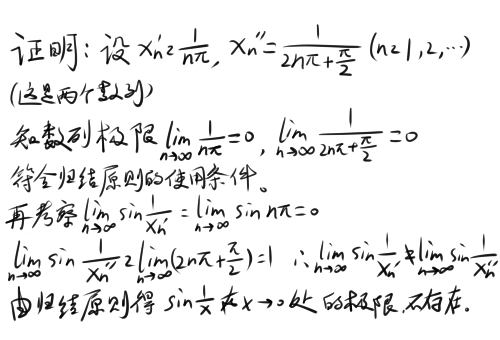“……的确是这样。”矽想到，继续往下看。“当然，归结原则还有一种更为简单的表示方法：
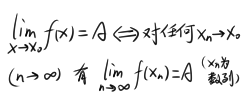。”“嗯……Isle刚才所讲的‘归结原则’，这种情况适用于x趋于某个定值的极限（而且是双侧极限），但是对于‘lim(x→+∞)’这种极限就不行了吧。”矽想，“Isle有没有给出这些情况下的归结原则呢。”
于是矽继续向下文找寻，然后发现了这样一段文字：“所谓归结原则，说起来就是把函数极限的问题归结为数列极限来处理。对于‘x趋近于正无穷’、‘x趋近于负无穷’一类的单侧极限问题，我就不赘述了，你应该可以自己归纳吧。毕竟现在已经快中午了，还有很多内容没有写上去呢。”
“竟然是这样，”矽想到，抬头看了看四周，又扭过头去瞥了眼屋外准备食物的人们，再回头思考起来。
“大概是这样的吧，”矽对着归结原则想到，“设f在U(+∞)这样一个正无穷领域内有定义。 lim(x→+∞)f(x)存在的充要条件是：对于任何含于 U(+∞)，且以+∞为极限的数列{x_n}，极限 lim(n→+∞)f(x_n)都存在且相等。”
“要是用它来证明 lim(x→+∞)cos(x)不存在……”矽又提笔把纸放在窗台上写到，“模仿上面的证明……
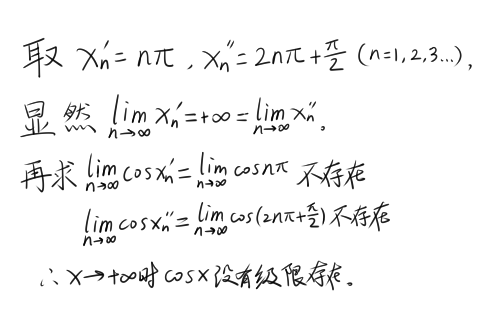。”“……当然，判断函数单侧极限时也可以不用归结原则……”
“哈？早说嘛。”矽想，就来看看如何不用归结原则考察单侧极限，虽然他的心里已有了底，“莫非是……”
“……相应对于数列极限的单调有界定理，关于函数的单侧极限问题也有相应的定理……”
“果然，”矽不禁说出了口，转念又想，“是不是‘柯西准则’也适用呢？”
“……那么你一定会想到柯西准则的概念是否也可以移植到函数极限上了吧。我提过‘ε-N定义’和‘ε-δ定义’是有关极限的数学里很重要的两个定义，而柯西准则就是更加完善的、形象的对极限问题的解决工具，它当然可以移植到函数极限中来……”
“……函数极限的柯西准则，设函数f在领域U゜(x_0;δ’)内有定义。 lim(x→x_0)f(x)存在的充要条件是：任给ε>0，存在正数δ(<δ’)，使得对任何x′x″∈U゜(x_0;δ’)有|f(x′)-f(x″)|<ε。这个定理的充分性可以由归结原则证明，必要性可由‘ε-δ定义’证明。用这个‘准则’的好处在于无需取特定的数列。”
矽思考了一下，打算用它来证明lim(x→0)sin(1/x)不存在：
由柯西准则可以得出，若函数f对某一个ε_0>0，对于任何可以取无限小的δ>0，使某一对x′x″∈U゜(x_0;δ’)有|f(x′)-f(x″)|≥ε，则f在x_0处的极限不存在。
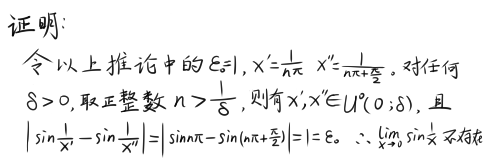写到这里，矽不禁感觉十分舒坦，站起身来，打算伸个懒腰。忽然，他听见门外传来了脚踏在石梯上的声音，并不断接近。“有人来了。”他想到，连忙把纸和信塞进了上衣的口袋里，手则塞在里面，站在窗口假装在看风景。就在此时，“咯吱”一声，门被推开了，甾走了进来，空气中顿时弥散出一股血腥味。甾对矽说：“矽，我们带了点野味回来，马上要开始烤了，你不下来吗？”
原来是动物的血腥味，矽想到，回头看着甾回答道：“烤肉还是等用餐时再吃吧。”
“那你在这儿一个人不会觉得无聊吗？”甾问，“还是说在一个人偷偷做些什么呢？”
“可能是一直以来一个人呆得久了吧，”矽说道，“况且这里风景不错，可以透过树林看到山顶，若有机会能上去就好了……”
“甾！”窗口外传来了络的声音，矽回头看向甾，说：“大概是叫你下去享用收获了吧。”
“那我走了，”甾说，关上房门跑下楼去。最近他感觉矽有点奇怪，并不只是刚才的事，而是从矽回来的几天就开始了，因为他总是一个人呆着，有时还神神叨叨的，谈论他的特长时也似乎有意在隐瞒什么，难道说……
“难道说矽受了那个叫‘Isle’的异乡人特长的影响，才有了特长？”甾想到，“或者说……他被催眠了？”这显然是异想天开。
矽在窗边坐下，待甾走了不久，一缕肉香从窗外传来，夹杂着油香和浆果的甜味。“已经开始了呀。”矽想着，继续看起了纸。
“……你以前应该接触过这个不等式吧。Sin(x)<x<tan(x)(0<x<π/2)，由单位圆结合三角函数可以推出……”
看到这里，矽立马就想起来他在8年级学三角函数时就学过这个不等式。
“……吧这个不等式每边除去sin(x)就变为了
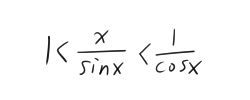，然后把整个式子取倒数（由于x的范围确定在(0，π/2)，因此不变号）可以得到
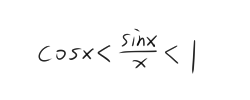。由于余弦函数cos(x)为偶函数，正弦函数和‘x’为奇函数（相除即为偶函数），于是这个不等式取‘-x’，也成立，那么这个不等式的自变量取值范围就被扩展到了U°(0;π/2)这个空心领域，且由lim(x→0)cos(x)=1可以得出，sin(x)/x在x趋近于0时，被余弦函数（cos(x)）和常函数（y=1）紧紧夹住，lim(x→0)sin(x)/x=1，这是我们直接观察原式所发现不了的，也是一个很重要的极限。”“嗯……”矽想到，“从原式上看，lim(x→0)sin(x)/x，分子趋近于0，分母也趋近于0，的确很不好解决。”
“……有了这个式子，我们就可以解决更多的极限求值问题了，比如说你可以求一下 lim(x→0)(1-cos(x))/x^2的值。”
矽看了看式子，会心一笑，立马写了出来：
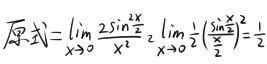。“……接下来，就是本章的最后一个内容，”Isle在信纸上这样写道，“在这之前的学习中，我们已经学习过数列极限lim(n→∞)(1+1/n)^n=e了，我们可以用归结原则把它引入函数极限……”
“是说lim(x→∞)(1+1/x)^x=e吧。”矽想到，“数列极限果真是和函数极限有着千丝万缕的联系啊。”
“……我们要验证lim(x→∞)(1+1/x)^x=e成立，即证 lim(x→+∞)(1+1/x)^x= lim(x→-∞)(1+1/x)^x=e成立。”
“什么？”看见这句话，矽有点吃惊，“原来这个式子在负无穷大处也成立呀。”
“先设数列……”
（此处暂时省略百余字的证明内容，我觉得你可能会看晕）
“矽！下来吃晚餐吧！”络的声音从楼下传来，使他从复杂的数学思考中惊醒，他才发觉，光线已经暗了下去，窗外已经看不见太阳了，所余的只有淡红的晖，鱼、肉、菜的香气混杂着愈发浓重，使他感到了饥饿。
“来了！”他对着窗外喊道，收起纸笔，走下楼去。
Twost滞留之地提示您：看后求收藏（卧龙小说网http://www.wolongxs.com），接着再看更方便。
好书推荐：《等我穿上小裙子你们就完蛋啦》、《好感度破亿的病娇缠上我了》、《我穿越到了全是女生的世界》、《我穿越到全是女孩子的世界》、《夜的命名术》、《无尽宇宙探索指南》、《深空彼岸》、《玲珑塔》、《星门》、《重启灾变》、
